Das Kartesische Produkt: Ein Grundbaustein Der Mathematik

Das Kartesische Produkt: Ein Grundbaustein der Mathematik

Verwandte Artikel: Das Kartesische Produkt: Ein Grundbaustein der Mathematik

Einführung

Mit Begeisterung werden wir uns durch das faszinierende Thema rund um Das Kartesische Produkt: Ein Grundbaustein der Mathematik vertiefen. Lassen Sie uns interessante Informationen zusammenfügen und den Lesern frische Perspektiven bieten.

Das Kartesische Produkt: Ein Grundbaustein der Mathematik

Das Kartesische Produkt, benannt nach dem französischen Mathematiker René Descartes, ist ein fundamentales Konzept in der Mathematik, das die Grundlage für viele weitere mathematische Strukturen und Anwendungen bildet. Es ermöglicht uns, aus mehreren Mengen eine neue Menge zu konstruieren, die alle möglichen Kombinationen der Elemente aus den ursprünglichen Mengen enthält. Dieses Konzept findet breite Anwendung in verschiedenen Bereichen der Mathematik, wie der Mengenlehre, der linearen Algebra, der Kombinatorik und der Informatik.

Grundlegendes Verständnis des Kartesischen Produkts

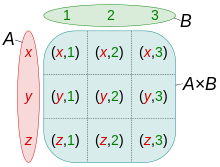
Die einfachste Art, sich das Kartesische Produkt vorzustellen, ist die Bildung von Paaren. Stellen Sie sich zwei Mengen vor: A und B. Das Kartesische Produkt von A und B, geschrieben als A × B, besteht aus allen möglichen Paaren, wobei das erste Element jedes Paares aus A und das zweite Element aus B stammt.

Beispiel:

• A = 1, 2
• B = a, b, c

Dann ist das Kartesische Produkt A × B:

• A × B = (1, a), (1, b), (1, c), (2, a), (2, b), (2, c)

Eigenschaften des Kartesischen Produkts:

• Kommutativität: Im Allgemeinen gilt A × B ≠ B × A, d.h. die Reihenfolge der Mengen ist wichtig.
• Assoziativität: (A × B) × C = A × (B × C).
• Neutralität: Es gibt eine neutrale Menge, die leere Menge ∅, sodass für jede Menge A gilt: A × ∅ = ∅ × A = ∅.

Anwendungen des Kartesischen Produkts

Das Kartesische Produkt findet in verschiedenen Bereichen Anwendung:

1. Mengenlehre:

• Potenzmenge: Die Potenzmenge einer Menge A ist die Menge aller Teilmengen von A, einschließlich der leeren Menge und der Menge A selbst. Die Potenzmenge kann als das Kartesische Produkt der Menge A mit sich selbst betrachtet werden, wobei jedes Element der Menge A entweder in der Teilmenge enthalten ist oder nicht.
• Relationen: Eine Relation zwischen zwei Mengen A und B ist eine Teilmenge des Kartesischen Produkts A × B. Zum Beispiel ist die Relation "kleiner als" zwischen den Mengen der natürlichen Zahlen 1, 2, 3 und 4, 5, 6 eine Teilmenge von 1, 2, 3 × 4, 5, 6, die alle Paare enthält, bei denen das erste Element kleiner ist als das zweite Element.

2. Lineare Algebra:

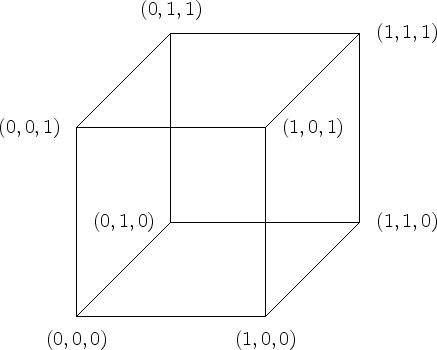
• Vektorraum: Ein Vektorraum ist ein mathematischer Raum, der aus Vektoren besteht. Ein Vektor kann als ein Tupel von Zahlen dargestellt werden. Die Menge aller möglichen Vektoren mit einer bestimmten Dimension kann als das Kartesische Produkt der entsprechenden Mengen von Zahlen betrachtet werden.
• Matrizen: Eine Matrix ist ein rechteckiges Schema von Zahlen. Die Menge aller möglichen Matrizen mit bestimmten Dimensionen kann als das Kartesische Produkt der entsprechenden Mengen von Zahlen betrachtet werden.

3. Kombinatorik:

• Permutationen: Eine Permutation ist eine Anordnung von Objekten. Die Anzahl der möglichen Permutationen von n Objekten ist n!. Die Menge aller möglichen Permutationen kann als das Kartesische Produkt der Menge der Objekte mit sich selbst n-mal betrachtet werden.
• Kombinationen: Eine Kombination ist eine Auswahl von Objekten aus einer Menge, wobei die Reihenfolge keine Rolle spielt. Die Anzahl der möglichen Kombinationen von n Objekten, wobei k Objekte ausgewählt werden, ist (n über k). Die Menge aller möglichen Kombinationen kann als das Kartesische Produkt der Menge der Objekte mit sich selbst k-mal betrachtet werden, wobei die Reihenfolge ignoriert wird.

4. Informatik:

• Datenstrukturen: Das Kartesische Produkt ist ein wichtiges Konzept in der Informatik, insbesondere bei der Arbeit mit Datenstrukturen. Beispielsweise kann ein Array als das Kartesische Produkt der Menge der Indizes mit der Menge der Werte betrachtet werden.
• Programmierung: In der Programmierung kann das Kartesische Produkt verwendet werden, um alle möglichen Kombinationen von Parametern zu generieren. Dies ist nützlich für die Entwicklung von Testfällen oder die Durchführung von Simulationen.

Bedeutung und Vorteile des Kartesischen Produkts

Das Kartesische Produkt ist ein wichtiges mathematisches Konzept, das zahlreiche Vorteile bietet:

• Strukturierung: Es ermöglicht die systematische Konstruktion neuer Mengen aus bestehenden Mengen, was die Untersuchung und Analyse von Beziehungen zwischen diesen Mengen vereinfacht.
• Generalisierung: Es bietet eine allgemeine Methode, um alle möglichen Kombinationen von Elementen aus mehreren Mengen zu erzeugen, was in verschiedenen Anwendungen nützlich ist.
• Klarheit: Es ermöglicht eine präzise und übersichtliche Darstellung von Beziehungen und Strukturen zwischen Mengen, was die Kommunikation und das Verständnis in der Mathematik erleichtert.
• Anwendbarkeit: Es findet breite Anwendung in verschiedenen Bereichen der Mathematik und darüber hinaus, was seine Bedeutung und Relevanz unterstreicht.

Häufig gestellte Fragen zum Kartesischen Produkt

1. Was ist der Unterschied zwischen A × B und B × A?

Das Kartesische Produkt ist im Allgemeinen nicht kommutativ, d.h. A × B ≠ B × A. Die Reihenfolge der Mengen ist wichtig, da die Elemente in den Paaren in einer bestimmten Reihenfolge angeordnet sind.

2. Kann das Kartesische Produkt einer Menge mit sich selbst gebildet werden?

Ja, das Kartesische Produkt einer Menge mit sich selbst ist möglich und wird oft verwendet, um die Menge aller möglichen Paare von Elementen aus dieser Menge zu bilden.

3. Was ist das Kartesische Produkt der leeren Menge?

Das Kartesische Produkt der leeren Menge mit einer beliebigen Menge ist immer die leere Menge.

4. Wie kann das Kartesische Produkt in der Praxis angewendet werden?

Das Kartesische Produkt findet in verschiedenen Bereichen Anwendung, wie der Mengenlehre, der linearen Algebra, der Kombinatorik und der Informatik. Es kann verwendet werden, um Beziehungen zwischen Mengen zu modellieren, Datenstrukturen zu erstellen, alle möglichen Kombinationen von Parametern zu generieren und vieles mehr.

5. Gibt es Einschränkungen bei der Anwendung des Kartesischen Produkts?

Das Kartesische Produkt kann für unendlich große Mengen verwendet werden, aber die resultierende Menge kann ebenfalls unendlich groß sein. In einigen Fällen kann die Berechnung des Kartesischen Produkts komplex oder sogar unmöglich sein.

Tipps zur Arbeit mit dem Kartesischen Produkt

• Visualisierung: Stellen Sie sich das Kartesische Produkt als eine Tabelle vor, wobei die Zeilen die Elemente der ersten Menge und die Spalten die Elemente der zweiten Menge repräsentieren. Die Zellen der Tabelle enthalten dann die Paare aus den beiden Mengen.
• Abstraktion: Konzentrieren Sie sich auf die allgemeine Definition des Kartesischen Produkts und nicht auf die konkreten Elemente der Mengen. Dies hilft Ihnen, das Konzept besser zu verstehen und auf verschiedene Anwendungen zu übertragen.
• Beispiele: Verwenden Sie konkrete Beispiele, um das Konzept des Kartesischen Produkts zu veranschaulichen. Dies hilft Ihnen, die Definition besser zu verstehen und die Anwendung in der Praxis zu erkennen.
• Verbindungen: Versuchen Sie, Verbindungen zwischen dem Kartesischen Produkt und anderen mathematischen Konzepten herzustellen. Dies hilft Ihnen, das Konzept in einen größeren Kontext einzubinden und seine Bedeutung zu verstehen.

Schlussfolgerung

Das Kartesische Produkt ist ein fundamentales mathematisches Konzept, das in verschiedenen Bereichen der Mathematik und darüber hinaus Anwendung findet. Es ermöglicht die Konstruktion neuer Mengen aus bestehenden Mengen, die systematische Analyse von Beziehungen zwischen Mengen und die Generierung aller möglichen Kombinationen von Elementen. Das Verständnis des Kartesischen Produkts ist daher für ein tiefgreifendes Verständnis der Mathematik und ihrer Anwendungen unerlässlich.

Abschluss

Daher hoffen wir, dass dieser Artikel wertvolle Einblicke in Das Kartesische Produkt: Ein Grundbaustein der Mathematik bietet. Wir hoffen, dass Sie diesen Artikel informativ und nützlich finden. Bis zum nächsten Artikel!